Matrices & Operators used in Perot's framework (1993, 2002). More...
Namespaces | |
| namespace | petibm::operators |
| Collections of factory functions of operators. | |
Functions | |
| PetscErrorCode | petibm::operators::createR (const type::Mesh &mesh, Mat &R) |
| Create a matrix of flux areas, | |
| PetscErrorCode | petibm::operators::createRInv (const type::Mesh &mesh, Mat &RInv) |
| Create a matrix of inversed flux areas, | |
| PetscErrorCode | petibm::operators::createMHead (const type::Mesh &mesh, Mat &MHead) |
| Create a matrix of cell widths of velocity points, | |
| PetscErrorCode | petibm::operators::createM (const type::Mesh &mesh, Mat &M) |
| Create a matrix | |
| PetscErrorCode | petibm::operators::createIdentity (const type::Mesh &mesh, Mat &I) |
| Create an identity matrix | |
| PetscErrorCode | petibm::operators::createGradient (const type::Mesh &mesh, Mat &G, const PetscBool &normalize=PETSC_TRUE) |
| Create a gradient operator, | |
| PetscErrorCode | petibm::operators::createDivergence (const type::Mesh &mesh, const type::Boundary &bc, Mat &D, Mat &DCorrection, const PetscBool &normalize=PETSC_TRUE) |
| Create a divergence operator, | |
| PetscErrorCode | petibm::operators::createLaplacian (const type::Mesh &mesh, const type::Boundary &bc, Mat &L, Mat &LCorrection) |
| Create a Laplacian operator, | |
| PetscErrorCode | petibm::operators::createConvection (const type::Mesh &mesh, const type::Boundary &bc, Mat &H) |
| Create a matrix-free Mat for convection operator, | |
| PetscErrorCode | petibm::operators::createBnHead (const Mat &Op, const PetscReal &dt, const PetscReal &coeff, const PetscInt &n, Mat &BnHead) |
| Create non-normalized matrix of approximated | |
| PetscErrorCode | petibm::operators::createBn (const Mat &Op, const Mat &R, const Mat &MHead, const PetscReal &dt, const PetscReal &coeff, const PetscInt &n, Mat &Bn) |
| Create normalized matrix of approximated | |
| PetscErrorCode | petibm::operators::createBn (const Mat &Op, const Mat &M, const PetscReal &dt, const PetscReal &coeff, const PetscInt &n, Mat &Bn) |
| Create normalized matrix of approximated | |
| PetscErrorCode | petibm::operators::createDelta (const type::Mesh &mesh, const type::Boundary &bc, const type::BodyPack &bodies, const delta::DeltaKernel &kernel, const PetscInt &kernelSize, Mat &Op) |
| Create a Delta operator, | |
Detailed Description
Matrices & Operators used in Perot's framework (1993, 2002).
An operator is a matrix, which will be the type of PETSc Mat. It may be a sparse matrix or a matrix-free matrix. Operators in CFD are based on the discretization of domain and boundary conditions, i.e. mesh. Therefore, all operator factories require a Mesh instance as an input, and most of them require a Boundary instance as another input.
Given that PetIBM now only supports staggered grid, most of the operators only make sense to staggered Cartesian CFD methods. So the operator factories can not create the operators for arbitrary fields. For example, createLaplacian can only create Laplacian for velocity fields because in our CFD framework (Perot 1993), only the Laplacian of velocity fields is required. This factory function cannot create Laplacian operators for arbitrary fields.
For operators taking boundary conditions, we decouple the interior part and boundary corrections. For example, applying a divergence operator to velocity will become
![]()
in which ![]() and
and ![]() represent divergence operators of interior points and ghost points (i.e., boundary correction), respectively.
represent divergence operators of interior points and ghost points (i.e., boundary correction), respectively.
Boundary conditions in PetIBM are implemented with ghost point schemes. Most of boundary conditions can be represented with, for example,
![]()
where ![]() and
and ![]() represent a ghost point and its corresponding interior point, respectively. Hence when we apply ghost point schemes to operators, the
represent a ghost point and its corresponding interior point, respectively. Hence when we apply ghost point schemes to operators, the ![]() part will get into the interior operator (e.g.
part will get into the interior operator (e.g. ![]() ), and the
), and the ![]() part will be decoupled into the boundary correction matrix, i.e.,
part will be decoupled into the boundary correction matrix, i.e., ![]() .
.
Here is an example code for creating a divergence operator and its boundary correction operator, and calculating the divergence of velocity.
Function Documentation
◆ createBn() [1/2]
| PetscErrorCode petibm::operators::createBn | ( | const Mat & | Op, |
| const Mat & | M, | ||
| const PetscReal & | dt, | ||
| const PetscReal & | coeff, | ||
| const PetscInt & | n, | ||
| Mat & | Bn | ||
| ) |
Create normalized matrix of approximated ![]() ,
, ![]() .
.
- Parameters
-
Op [in] Implicit operator 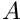 .
. M [in] The 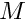 matrix as defined in
matrix as defined in 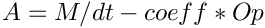 .
. dt [in] Time-step size. coeff [in] Time-scheme coefficient for the implicit operator. n [in] an integer; the order of Bn. Bn [out] Matrix 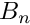 .
.
Similar to createBnHead, except that A is now defined as
![]()
Definition at line 131 of file createbn.cpp.
◆ createBn() [2/2]
| PetscErrorCode petibm::operators::createBn | ( | const Mat & | Op, |
| const Mat & | R, | ||
| const Mat & | MHead, | ||
| const PetscReal & | dt, | ||
| const PetscReal & | coeff, | ||
| const PetscInt & | n, | ||
| Mat & | Bn | ||
| ) |
Create normalized matrix of approximated ![]() ,
, ![]() .
.
- Parameters
-
Op [in] Implicit operator 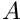 .
. R [in] Matrix to define 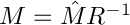 .
. MHead [in] Matrix to define 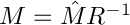 .
. dt [in] Time-step size. coeff [in] Time-scheme coefficient for the implicit operator. n [in] Truncation index of the Taylor series. Bn [out] Matrix, 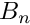 .
.
Similar to createBnHead, except that A is now defined as
![]()
where
![]()
Definition at line 98 of file createbn.cpp.
◆ createBnHead()
| PetscErrorCode petibm::operators::createBnHead | ( | const Mat & | Op, |
| const PetscReal & | dt, | ||
| const PetscReal & | coeff, | ||
| const PetscInt & | n, | ||
| Mat & | BnHead | ||
| ) |
Create non-normalized matrix of approximated ![]() ,
, ![]() .
.
- Parameters
-
Op [in] Implicit operator 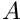 .
. dt [in] Time-step size. coeff [in] Time-scheme coefficient for the implicit operator. n [in] Truncation index of the Taylor series. BnHead [out] Operator 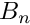 .
.
![]() is defined as *
is defined as *
![]()
where ![]() is an identity matrix,
is an identity matrix, ![]() is the summation of all implicit operators, and
is the summation of all implicit operators, and ![]() is the coefficient from temporal integration. For example, for the case of Adams-Bashforth for convective terms and Crank-Nicolson for diffusion term,
is the coefficient from temporal integration. For example, for the case of Adams-Bashforth for convective terms and Crank-Nicolson for diffusion term,
![]()
If the implicit part is more complicated, there may be not only one coefficient for each implicit operator. Then, in order to use this function, we may need to incorporate coefficients and all implicit operators into a big implicit operator before calling this function. And then set ![]() as
as ![]() . For example, if an
. For example, if an ![]() is defined as
is defined as
![]()
then we need to first define
![]()
so that ![]() can have the form of
can have the form of
![]()
.
Definition at line 19 of file createbn.cpp.
◆ createConvection()
| PetscErrorCode petibm::operators::createConvection | ( | const type::Mesh & | mesh, |
| const type::Boundary & | bc, | ||
| Mat & | H | ||
| ) |
Create a matrix-free Mat for convection operator, ![]() .
.
- Parameters
-
mesh [in] Structured Cartesian mesh object. bc [in] Data object with boundary conditions. H [out] Operator 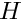 .
.
Though this matrix-free operator is a PETSc Mat, not all PETSc Mat functions can be applied to it because we only register MatMult and MatDestroy functions in PetIBM.
If ![]() is the composite velocity vector, then the multiplication
is the composite velocity vector, then the multiplication ![]() will return the convection terms at velocity points.
will return the convection terms at velocity points.
Definition at line 372 of file createconvection.cpp.
◆ createDelta()
| PetscErrorCode petibm::operators::createDelta | ( | const type::Mesh & | mesh, |
| const type::Boundary & | bc, | ||
| const type::BodyPack & | bodies, | ||
| const delta::DeltaKernel & | kernel, | ||
| const PetscInt & | kernelSize, | ||
| Mat & | Op | ||
| ) |
Create a Delta operator, ![]() .
.
- Parameters
-
mesh [in] Structured Cartesian mesh object. bc [in] Data object with boundary conditions. bodies [in] Data object with the immersed boundaries. kernel [in] Regularized delta kernel to use. kernelSize [in] Size of the kernel. Op [out] Matrix 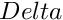 .
.
In ![]() , rows represent Lagrangian points, while columns represent velocity mesh points.
, rows represent Lagrangian points, while columns represent velocity mesh points.
An entry in ![]() , says
, says ![]() , is defined as
, is defined as
![]()
where ![]() and
and ![]() represent the coordinates of the
represent the coordinates of the ![]() -th Eulerian grid point and the
-th Eulerian grid point and the ![]() -th Lagrangian point, respectively.
-th Lagrangian point, respectively. ![]() is discretized delta function following Roma et. al. (1999).
is discretized delta function following Roma et. al. (1999).
Definition at line 34 of file createdelta.cpp.
◆ createDivergence()
| PetscErrorCode petibm::operators::createDivergence | ( | const type::Mesh & | mesh, |
| const type::Boundary & | bc, | ||
| Mat & | D, | ||
| Mat & | DCorrection, | ||
| const PetscBool & | normalize = PETSC_TRUE |
||
| ) |
Create a divergence operator, ![]() , and corresponding boundary correction,
, and corresponding boundary correction, ![]() , for velocity fields.
, for velocity fields.
- Parameters
-
mesh [in] Structured Cartesian mesh object. bc [in] Data object with the boundary conditions. D [out] Divergence operator 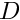 .
. DCorrection [out] Operator for boundary corrections, 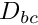 .
. normalize [in] Use PETSC_TRUE to normalize operator (default is PETSC_TRUE).
PETSc matrix D should not be created before calling this function.
If normalize=PETSC_TRUE (which is default), then the divergence operator, ![]() , will only contain
, will only contain 0 and 1.
The divergence operator calculates the divergence of velocity on pressure points. The complete divergence operator is ![]() . However, the boundary correction,
. However, the boundary correction, ![]() , represents the constant coefficients (it means the coefficients that have nothing to do with interior points, though it may still be time-dependent) in ghost point schemes, so it's safe to put the boundary correction to right-hand side in a linear system.
, represents the constant coefficients (it means the coefficients that have nothing to do with interior points, though it may still be time-dependent) in ghost point schemes, so it's safe to put the boundary correction to right-hand side in a linear system.
Definition at line 103 of file createdivergence.cpp.
◆ createGradient()
| PetscErrorCode petibm::operators::createGradient | ( | const type::Mesh & | mesh, |
| Mat & | G, | ||
| const PetscBool & | normalize = PETSC_TRUE |
||
| ) |
Create a gradient operator, ![]() , for pressure field.
, for pressure field.
- Parameters
-
mesh [in] Structured Cartesian mesh object. G [out] 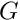 matrix.
matrix. normalize [in] Use PETSC_TRUE to normalize the matrix (default is PETSC_TRUE).
Petsc matrix G should not be created before calling this function.
If normalize=PETSC_TRUE (which is default), then the gradient operator, ![]() , will only contain
, will only contain 0 and 1.
This gradient operator doesn't require boundary conditions because we only need gradient of pressure at interior velocity points (see Perot 1993). And it can only be applied to pressure field. For example:
Definition at line 36 of file creategradient.cpp.
◆ createIdentity()
| PetscErrorCode petibm::operators::createIdentity | ( | const type::Mesh & | mesh, |
| Mat & | I | ||
| ) |
Create an identity matrix ![]() for velocity fields.
for velocity fields.
- Parameters
-
mesh [in] Structured Cartesian mesh object. I [out] 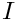 matrix.
matrix.
PETSc matrix I should not be created before calling this function.
Definition at line 210 of file creatediagmatrix.cpp.
◆ createLaplacian()
| PetscErrorCode petibm::operators::createLaplacian | ( | const type::Mesh & | mesh, |
| const type::Boundary & | bc, | ||
| Mat & | L, | ||
| Mat & | LCorrection | ||
| ) |
Create a Laplacian operator, ![]() , and boundary correction,
, and boundary correction, ![]() for velocity fields.
for velocity fields.
- Parameters
-
mesh [in] Structured Cartesian mesh object. bc [in] Data object for the boundary conditions. L [out] Laplacian operator 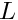 .
. LCorrection [out] Operator for boundary corrections, 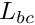 .
.
PETSc matrix L should not be created before calling this function.
The complete Laplacian is ![]() . The boundary correction represents the constant coefficients (the coefficients that have nothing to do with interior velocity points) in ghost point schemes. So it's often seen the boundary correction
. The boundary correction represents the constant coefficients (the coefficients that have nothing to do with interior velocity points) in ghost point schemes. So it's often seen the boundary correction ![]() on right-hand side of a system, while
on right-hand side of a system, while ![]() on left-hand side.
on left-hand side.
Definition at line 170 of file createlaplacian.cpp.
◆ createM()
| PetscErrorCode petibm::operators::createM | ( | const type::Mesh & | mesh, |
| Mat & | M | ||
| ) |
Create a matrix ![]() .
.
- Parameters
-
mesh [in] Structured Cartesian mesh object. M [out] 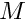 matrix.
matrix.
PETSc matrix M should not be created before calling this function.
In some CFD schemes, the combination of ![]() and
and ![]() is used frequently. So this function creates a matrix
is used frequently. So this function creates a matrix ![]() for convenience.
for convenience.
Definition at line 180 of file creatediagmatrix.cpp.
◆ createMHead()
| PetscErrorCode petibm::operators::createMHead | ( | const type::Mesh & | mesh, |
| Mat & | MHead | ||
| ) |
Create a matrix of cell widths of velocity points, ![]() .
.
- Parameters
-
mesh [in] Structured Cartesian mesh object. MHead [out] 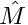 matrix.
matrix.
PETSc matrix MHead should not be created before calling this function.
Operator ![]() represents the cell width of velocity points. The cell width of a
represents the cell width of velocity points. The cell width of a ![]() -velocity point with index
-velocity point with index ![]() , for example, is
, for example, is ![]() , and the cell width of
, and the cell width of ![]() -velocity at
-velocity at ![]() is
is ![]() .
.
The multiplication of ![]() and
and ![]() returns the cell volumes of velocity points, i.e.,
returns the cell volumes of velocity points, i.e., ![]() .
.
Definition at line 150 of file creatediagmatrix.cpp.
◆ createR()
| PetscErrorCode petibm::operators::createR | ( | const type::Mesh & | mesh, |
| Mat & | R | ||
| ) |
Create a matrix of flux areas, ![]() .
.
- Parameters
-
mesh [in] Structured Cartesian mesh object. R [out] 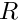 matrix.
matrix.
PETSc matrix R should not be created before calling this function.
Operator ![]() represents the flux areas of velocity points. For example, if
represents the flux areas of velocity points. For example, if ![]() is vector of velocity flux, and
is vector of velocity flux, and ![]() is velocity vector, then
is velocity vector, then ![]() .
.
- See also
- petibm::operators::createRInv
Definition at line 90 of file creatediagmatrix.cpp.
◆ createRInv()
| PetscErrorCode petibm::operators::createRInv | ( | const type::Mesh & | mesh, |
| Mat & | RInv | ||
| ) |
Create a matrix of inversed flux areas, ![]() .
.
- Parameters
-
mesh [in] an instance of petibm::type::Mesh. RInv [out] a PETSc Mat; returned matrix 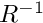 .
.
PETSc matrix RInv should not be created before calling this function.
Operator ![]() is the inverse of
is the inverse of ![]() . And it has relationship
. And it has relationship ![]() , in which
, in which ![]() and
and ![]() are as defined in petibm::operators::createR.
are as defined in petibm::operators::createR.
- See also
- petibm::operators::createR
Definition at line 120 of file creatediagmatrix.cpp.